Regularnie obserwuję pewną trudność jaką sprawia wielu ludziom, z jednej strony stosowanie systemów notacyjnych a z drugiej samo modelowanie. Wspólną częścią obu tych obszarów jest abstrahowanie od szczegółów. Praktycznie każdy mój klient i bardzo często, analitycy i projektanci developerów realizujących projekty które nadzoruję, zadają mi pytania: a gdzie zobaczę to, że zamówienie może być dla innego produktu i innego segmentu….. itp. Innymi słowy: na dowolnym etapie pracy padają pytania o bardzo detaliczne szczegóły konkretnych operacji. Co prawda, jak to mawiają “diabeł tkwi w szczegółach”, z czym wypada się zgodzić, ale to dokładnie ten właśnie diabeł niszczy projekty prowadząc nie raz do “utraty panowania nad szczegółowością projektu”. Dokładnie dwa lata temu opisywałem modelowanie problem detali w artykule Gdzie są te cholerne szczegóły, a kwestie zasad (reguł) działania aplikacji w niedawnym artykule Mechanizm działania. Dzisiaj będzie o modelach i abstrakcjach.
Modele a abstrakcje
Modelowanie ma dwa aspekty: projektowanie jako tworzenie modelu przyszłej (projektowanej) rzeczywistości oraz analiza jako tworzenie modelu badanej, istniejącej rzeczywistości. Model jako taki nie jest abstrakcją czegoś, jest uproszczonym obrazem lub opisem z określonej perspektywy, ale zachowującym określone cechy rzeczywistości. Model z definicji jest zawsze uproszczeniem, innymi słowy, jest pozbawiony określonych szczegółów, tych które w danym zastosowaniu modelu (kontekst) są nieistotne. Pojęcia model i abstrakcja są często mylone, bywa że stosowane zamiennie, co jest bardzo dużym błędem.
Podstawowym narzędziem analizy jest proces redukowania szczegółów, w przeciwnym wypadku pracochłonność opracowania modelu i późniejsza jego analiza, może wręcz uniemożliwić rzetelne ich przeprowadzenie, może być to nawet niewykonalne z uwagi na ich nadmierną złożoność. Słownik j. polskiego PWN podaje następujące definicje:
abstrakcja: pojęcie ogólne, niemające odpowiednika w żadnym konkretnym przedmiocie;
model: konstrukcja, schemat lub opis ukazujący działanie, budowę, cechy, zależności jakiegoś zjawiska lub obiektu;
Pomiędzy pojęciami abstrakcja i model jest pewna kluczowa różnica: abstrakcja to pojęcie zaś model to opis mechanizmu, jego konstrukcja, działanie, budowa. Prosty przykład: nazwane prostokąty na typowym diagramie struktury organizacyjnej to abstrakcje komórek organizacyjnych i osób w nich zatrudnionych, prostokąty te wraz z liniami je łączącymi stanowią, jako całość, model podległości zasobów w organizacji. Nieco ponad pół roku temu opisałem to w artykule Diagram obiektów czyli bottom-up:
Generalnie rzecz w tym, by pokazać to co wiemy czyli konkretne nazwane egzemplarze ?tych rzeczy?, o których ktoś mówi lub które obserwujemy. To egzemplarze i ich specyfikacja (nazwy, cechy itp.). Innymi słowy
diagram obiektów służy do pokazania konkretnego, obserwowalnego stanu rzeczy.
Jeżeli więc z jakiegoś powodu nie możemy operować uogólnieniami (klasy) bo nie posiadamy odpowiedniej wiedzy lub jest ona zbyt uboga, analizę można prowadzić ?od dołu? czyli mając szczegóły uogólniać je. Poważną zaletą tej metody jest łatwość weryfikacji modelu przez ?klienta?. Większość ludzi nie radzi sobie z abstrakcjami (np. metamodele): modele budowane z użyciem diagramów klas to uogólnienia: opisują klasy a nie konkretną rzeczywistość. Diagramy obiektów (instancje klas) to nic innego jak modele ?konkretnych sytuacji? z życia. (Źródło: Diagram Obiektów | Jarosław Żeliński IT-Consulting)
Poziomy abstrakcji w UML
Notacja UML pozwala na modelowanie na obu wyżej wymienionych poziomach. W ramach [[MOF]]/[[UML]] wyróżniamy łącznie cztery poziomy uogólnienia oznaczone od M0 do M3. M0 to świat rzeczywistych bytów. M1 to model w którym konkretne rzeczywiste byty zastępuje się ich abstrakcjami (np. nazwane prostokąty), których jest tyle ile rzeczywistych obiektów. Poziom M2 to metamodel, czyli wszystkie nazwane elementy klasyfikujemy i zastępujemy klasyfikatorami. Obiekty mające pewne ustalone wspólne cechy (całą ich grupę) zastępujemy jednym klasyfikatorem. Np. na poziomie M1 model drużyny piłkarskiej będzie zawierał 11 nazwanych obiektów (tu prostokąt to abstrakcja zawodnika). Na poziomie M2 model tej drużyny to była by już tylko klasa Zawodnik, zapewne jednym z jej atrybutów byłoby imię i nazwisko oraz numer zawodnika a drugim jego rola (bramkarz lub zawodnik w polu, to decyduje o jego zachowaniu). Na najwyższym poziomie M3 mamy tylko zdefiniowane pojęcie klasyfikatora.
Notacja UML pozwala na modelowanie (tworzenie modeli i metamodeli) na poziomach M1 i M2 (poziom M3 to definicja klasyfikatora w UML, polecam tu książkę Model-Driven Software Engineering…). Poniżej diagram obrazujący te cztery poziomy oraz taksonomie diagramów w UML 2.5 gdzie diagramy zostały skojarzone z odpowiadającymi im poziomami abstrakcji.
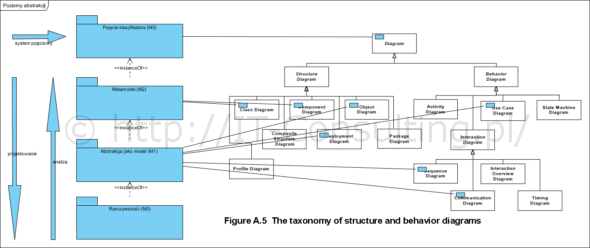
Warto o tym pamiętać, głównie z tego powodu, że diagram klas notacji UML jest powszechnie nadużywany, wiele modeli, szczególnie dokumentujących stan faktyczny konkretnej aplikacji i wdrożenia, powinno być diagramami obiektów i wdrożenia a nie diagramami klas czy komponentów, bo te ostanie to jedynie metamodele. Warto też wiedzieć, że kod programu to metamodel tego co zostanie wytworzone w pamięci komputera (bo to jest model rzeczywostości), po uruchomieniu tego programu. W kodzie np. gry będzie klasa zawodnik, ale po uruchomieniu gry komputerowej, w pamięci będzie 11 wygenerowanych z tych klas obiektów, reprezentujących zawodników drużyny.
Na powyższym diagramie, po jego lewej stronie, pokazałem także, że projektowanie czegoś jest rozpoczynaniem pracy od tworzenia określonej abstrakcji pomysłu (z reguły obiekty a nie klasy). Analiza stanu rzeczywistego to tworzenie tej abstrakcji na bazie obserwacji analizowanej rzeczywistości.

Projekty w obszarze inżynierii oprogramowania, tworzone w duchu paradygmatu obiektowego to:
- analiza rzeczywistości i zbudowanie jej obiektowej abstrakcji (diagram obiektów),
- określenie, który obszar rzeczywistości zostanie zastąpiony oprogramowaniem (np. papierowe kartoteki w bibliotece),
- zbudowanie metamodelu wybranego obszaru : to model dziedziny (diagram klas)
Pierwszy punkt to element analizy systemowej: tworzenie obiektowego modelu tego co jest analizowane. Podejście obiektowe do analizy i projektowania więc:
…pozwala wyjść od konkretnego rzeczywistego ?stanu świata? i opracować na jego podstawie model pojęciowy i metamodel. To bardzo pomocna technika. Warto pamiętać, że to co nie raz nazywane jest ?modelem dziedziny? jednak nim nie jest. (Źródło: Diagram Obiektów | Jarosław Żeliński IT-Consulting)