Wprowadzenie
Do dzisiaj nie wiedziałem, że świat od wielu lat jest podzielony na zwolenników tych dwóch różnych wyników. Dowiedziałem się o tym, gdy zupełnie niechcący, po opublikowaniu poniższego mema:
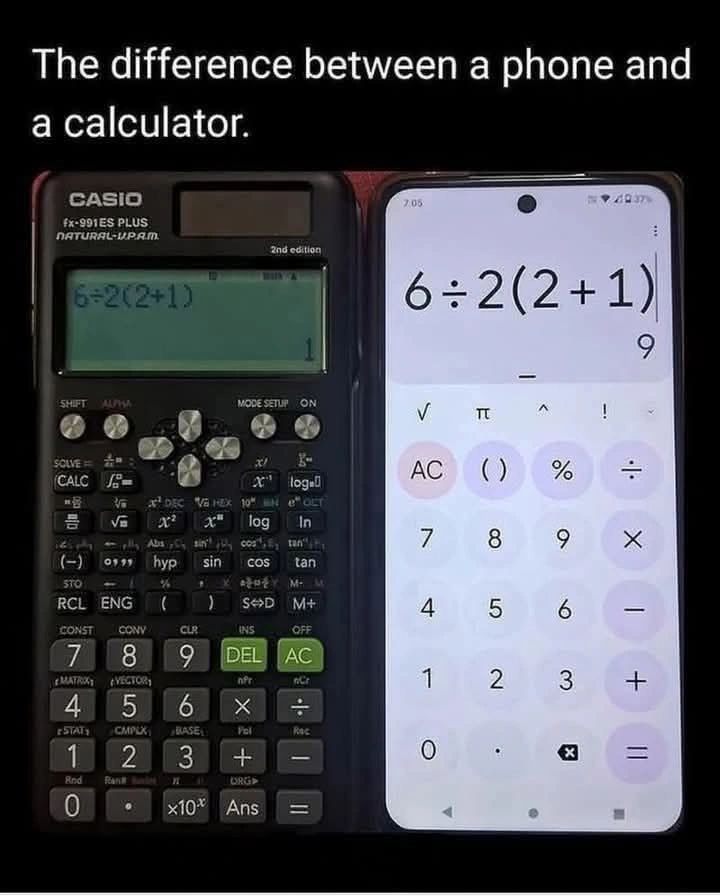
rozpętałem burzliwą dyskusje ale tylko z kilkoma osobami. Na końcu artykułu wyjaśnienie dlaczego warto czasem rzucić się w wir takich problemów. Kalkulatory naukowe pokazują “1” i warto sie zastanowić dlaczego.
Równania i podstawianie jako metoda
Podstawianie to jedna kluczowych zasad w logice i matematyce. Służy to rozwiązywania równań ale także do testowania definicji. Prosty przykład:
jeżeli
y=2x
oraz
x=5
to wstawiać 5 w miejsce x
y=2*5
czyli
y=10
Myślę, że to nie budzi niczyich wątpliwości. O tym zapewne wie każdy kto ma podstawowe wykształcenie. Pewne trudności zaczynają sprawiać nawiasy.
y=2(a+x) + 5(5 – x)
Z tym równaniem raczej mało kto będzie miał problem, bo “jak wiadomo” najpierw mnożenie potem dodawanie. Można to nadmiarowo zapisać tak:
y=(2(a+x)) + (5(5 – x))
Tu
y=2(a+x) * 5(5 – x)
Tu też raczej każdy uzna, że to to samo co
y=(2(a+x)) * (5(5 – x))
Idźmy dalej. Jeżeli
2(a+x) = C
oraz
y=2(a+x) * 5(5 – x)
Możemy napisać, że:
y=C* 5(5 – x)
Z mnożeniem nie ma problemu, więc mała zmiana:
y=C/5(5 – x)
Cofamy sie krok:
y=2(a+x)/5(5 – x)
W jakiej teraz kolejności wykonacie to działanie? Zapiszmy to inaczej:
y=2(a+x):5(5 – x)
Czy to jest to samo? Proste szkolne zasady mówią, że:
Reguła: Kolejność wykonywania działań
Działania wykonujemy w następującej kolejności:
1. najpierw wykonujemy działania w nawiasach,
2. następnie mnożenie lub dzielenie,
3. na końcu dodawanie lub odejmowanie.
(https://zpe.gov.pl/a/kolejnosc-wykonywania-dzialan/D18isdYPe)
Problem stwarza da druga i słowo lub bo daje na dowolność. Dodawanie i odejmowanie to tak naprawdę jedna i ta sama operacja: sumowanie uwzględniające znak: 5 + (-3) = 5 -3 = (-3) + 5 = 2. Nie mamy co do tego żadnych wątpliwości. Jednak w przypadku mnożenie i dzielenia to tak nie działa bo dzielnie to mnożenie przez odwrotność (dodatkowe działanie: odwrotność). Dlatego mamy przemienność dodawania:
3+2= 5 i 2+3= 5 ale 3-2= 1 ale już nie piszemy 2-3=1 tylko (-2) +3=1
rzecz w tym, że znakomita większość ludzi intuicyjnie pomija znaki i nawiasy wszędzie tam, gdzie “nie budzi to wątpliwości”. Bo realnie mamy
3+2= 5 czyli (+3) + (+2) = (+5)
Ale tak raczej już nikt nie napisze: tak działa intuicja, wyuczone uproszczenia. Niestety bywa, że te uproszczenia szkodzą.
Mamy przemienność mnożenia ale nie mamy “przemienności dzielenia”. Prawdą jest, że
3*2 = 2*3 = 6
ale nie jest prawda, że
jeżeli 6:2 = 3 to 2:6 = 3
Dygresja: Zwróćcie także uwagę, że wstawiam (nie ja jeden) w pewnych miejscach odstępy, nie napisałem 3*2=2*3=6 tylko 3*2 = 2*3 = 6). To naszemu mózgowi ułatwia interpretacje treści: mózgi nasze są wykształcone na prozie, są oswojone ze spacjami między słowami, to ułatwia interpretację czyli poprawne rozumienie (słynne spory o “nie z czasownikami piszemy osobno”. Możemy powiedzieć, że ktoś:
- “nie jest grzeczny”,
- lub że “jest niegrzeczny”.
Pierwsze to jego (np. aktualne) zachowanie, a drugie to jego cecha. To nie jest to samo.
Wracamy do dzielenia.
4:2 = 2 ale 2:4 = 0,5
i tu nie mamy takiej możliwości jak w sumowaniu (zwróćcie uwagę na to, że to 3+2=5 nazywamy zwyczajowo dodawaniem zaś to 3-2=1 nazwiemy odejmowaniem, mało kto w obu przypadkach użyje słowa “sumowanie”. Jak nazwiecie to: 3+(-2) = 1.
W dzieleniu, jeżeli 4:2 = 2 to 4*1:2 a także 4*(1:2). Jednak mały zgrzyt: dla 4*1:2 możemy powiedzieć, że “między cztery a jeden jest mnożenie, ale nie mozna tego powiedzieć tu 4*(1/2). Tu wynik jest taki sam ale nie są to takie same wyrażenia.
Sporne wyrażenie
6:2(2+1)=?
W przypadku dodawania nie mamy wątpliwości, że 2+1 to samo co (+2)+(+1) bo w sumowaniu znak liczby zawsze jest a intuicyjnie brak plusa traktujemy jak plus. Problem polega na tym, że ta intuicja nie występuje przy mnożeniu i dzieleniu. Powyższe można napisać tak:
6:2*3
i każdemu jako wynik wyjdzie 9, pozostaje pytanie czy wolno bezkarnie w ten sposób usunąć ten nawias? Na bazie powyższych wyjaśnień sugeruję inną kolejność: najpierw działania z nawiasami (a nie “w nawiasach”, bo to nie to samo) potem reszta:
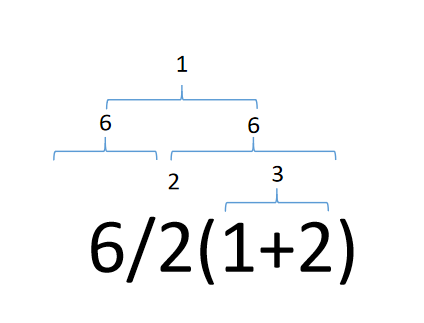
Bo faktycznie
2(1+2)= 6
Ale czy dodanie na początku 6 oraz znaku : to zmienia? Mamy zasadę przemienności mnożenia ale nie ma zasady przemienności dzielenia bo 6:3 to nie to samo co 3:6. Pytanie kluczowe: jaki znak mamy przed liczbą 6? Powiemy, że to +6, *6 czy :6? Powiemy, że to wyrażenie można zapisać 6:(+2)(1+2) , jaka tu kolejność działań obowiązuje? Działania na ułamkach mówią, że dzielenie ma pierwszeństwo przed mnożeniem. 3*4:2 czy 3*4/2 ale 3:4*2 jako 3/4*2? Innymi słowy znak dzielenia to “domyślny nawias”: 3:(4*2), i teraz jeżeli 1+1=2 to 3:4*2 to to samo co 3:4(1+1) bo pamiętamy czym jest podstawianie.
Niewątpliwie w sumowaniu mamy dowolność kolejności sumowania ciągu liczb (uwzględniając ich znak), ale nie mamy te dowolności w mnożeniu i dzieleniu bo najpierw musielibyśmy wszystkie dzielenia zastąpić mnożeniem przez odwrotność, czyli każda liczba x poprzedzona znakiem : to 1/x. Czyli
3/4*2 = 3 * 1/4 * 2 czy jednak 3 * (1/4) * 2
a teraz trudniejsze: 3:2:4:6 zamieniany na 3*(1/2)*(1/4)*(1/6). A co z pierwszą liczbą? Czy możemy pierwszą 3 bezkarnie przenieść na koniec? Jeżeli tak to z jakim znakiem, mnożenia czy dzielenia? To znaczy, że w przypadku mnożenia i dzielenia mnie mamy pełnej przemienności albo musimy założyć, że pierwsze liczba to zawsze mnożnik, pytanie na jakiej podstawie to założenie? Dlatego albo nie mamy podstaw by uznać pełną przemienność mnożenia albo musimy założyć brak znaku to z zasady mnożenie czyli 3 to zawsze to samo co *3 , a to już jest problematyczne…
Przypomnijmy:
6:2(2+1)=?
Jedni twierdzą, że
6:2*(2+1) = (6:2)*(2+1) = 3*(2+1) = 3*3 = 9
inni że
6:2(2+1) = 6 : (2*(3)) = 6 : 6 = 1
Obie grupy “dodały sobie” dodatkowe nawiasy by bronić każda swojej tezy. Pozostaje pytanie, ktore dodane nawiasy są uprawnione? Zróbmy test wykorzystując zasadę podstawiania w algebrze.
jeżeli x=2+1 to 6:2(2+1) = 6:2(x)
oraz
jeżeli x=2+1 to x=3
Testujemy dwie hipotezy rozwiązując równania:
6:2(x)=9
oraz
6:2(x)=1
Pozostaje pytanie czy prawdą jest, że 6:2(x) = 3(x) bo cały ten spór, to spór pytanie:
Czy prawdę jest, że a:b(x) = a:(b(x))
To “spór” między arytmetyką a algebrą (patrz Podsumowanie na końcu).
Przetestujmy te podejścia. Przemienność mnożenia wymaga traktowania dzielnie jak mnożenia przez odwrotność. Czy wolno nam napisać:
a:b(x) = a * (1/b) * (x)
Jeżeli uznamy zasadę, mówiącą, że najpierw działania z nawiasami, a nawias to nie “zwykłe mnożenie” to nie jest to prawdą. Dlatego
a:b(x) = a * (1/(b * (x))
W zapisie 6:2(2+1) wyrażenia “2(2+1)” nie wolno rozdzielać na proste mnożenie “2* (2+1)”. Dlatego w tak zwanych kalkulatorach naukowych wyniki są jak w powyższym memie: 6:2(2+1)=1 wg. zasady:
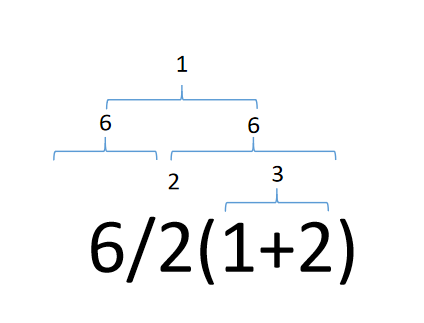
Znajdziecie też źródła gdzie “2(x) : 3(x)” to to samo co “2(x) : 3 * (x)”, to książki do arytmetyki. Pozostaje pytanie czy mamy tu proste czterodziałaniowe rachunki, czy jednak coś więcej czyli “logikę zdań” będąca częścią algebry. Czy zawsze musimy ładować wszędzie tę wredną logikę? Uważam, że tak choćby dla utrzymania spójności, bo bez tego w szkole podstawowej wychodzi, że
6:2(2+1)=9
a na studiach w kalkulatorach naukowych, że
6:2(2+1)=1
Podsumowanie
Ciekawy wykład na ten temat: What Is the Answer to That Stupid Math Problem on Facebook?
If it “feels” natural to you that implied multiplication takes precedence over division (whether because it’s next to a parentheses or not), then you would get 6 ÷ 2(1+2) = 6 ÷ (2(3)) = 6 ÷ 6 = 1. That answer would be incorrect on most U.S. standardized tests, but you wouldn’t necessarily be wrong. (Insert rant against standardized tests here.) You would just be in the minority about which convention you’re using.
Jeśli “czujesz”, że mnożenie ma pierwszeństwo przed dzieleniem (czy to dlatego, że jest obok nawiasu, czy nie), to otrzymałbyś 6 ÷ 2(1+2) = 6 ÷ (2(3)) = 6 ÷ 6 = 1. Ta odpowiedź byłaby niepoprawna w większości standaryzowanych testów w USA, ale niekoniecznie byłaby błędna. (Byłbyś po prostu w mniejszości, jeśli chodzi o konwencję, której używasz).
Wszyscy kończyliśmy szkołę podstawową i uczyliśmy się arytmetyki. Tylko niektórzy kończyli studia na których wykładano algebrę (ja starałem się wyjaśnić wynik stosując reguły algebry). W matematyce mamy (SJP):
arytmetyka: nauka o liczbach i działaniach na nich wykonywanych; też: dział zajmujący się teorią rachunków w zbiorach z określonymi działaniami
oraz
algebra: dział matematyki zajmujący się m.in. rozwiązywaniem równań zapisanych za pomocą symboli literowych
Dlatego warto do takiego wzoru spróbować “przyłożyć” realny, a przynajmniej możliwy, fakt i wtedy dopiero go intepretować. Matematyka to język, a nie “nauka przyrodnicza” (Słowo „scientific” odnosi się głównie do nauk
eksperymentalnych, takich jak nauki przyrodnicze i medyczne). Innymi słowy, opisywanie w jakimkolwiek języku, rzeczy niemożliwych do weryfikacji w praktyce, moim zdaniem mija się z celem. Dlatego ogromny sens w nauczaniu matematyki mają tak zwane “zadania z treścią”, czyli realne sytuacje, w których matematyki używamy do ich opisu, by rozwiązać problem.
Inna ciekawa dyskusja także z algebraicznym wyjaśnieniem:
Milana · Studied at High School Mathematics
There is no multiplication sign between 2 and (2+1), therefore it is considered a single mathematical expression as 2X.
6 ÷ 2(3) = 6 ÷ 6 = 1 ANSWER
Like 6 ÷ 2X = 3/X right answer.
No way: 6/2 * X = 3X wrong answer
In this case X = 3 => 3/3 = 1 right answer
3* 3 = 9 wrong answer
oraz
Now you should be able to figure easily that 6÷2a = 3/a.
Let a=2+1 and we have:
6÷2(2+1) = 3/(2+1) = 3/3 = 1.
To “viralowe” zadanie matematyczne, będące tematem tego artykułu, są doskonałym przykładem tego, by takich sztucznych, oderwanych od realiów zadań sobie nie stawiać.
Logika zdań
Dla zainteresowanych podobnymi problemami logiki w analizach biznesowych, kilka słów o zasadzie podstawiania w ontologii i w tak zwanych zdaniach prawdziwych, czyli nie raz tak zwanych regułach biznesowych w projektach naszych systemów.
W logice zdań metodą podstawiania testujemy definicje pojęć, zasada ta mówi, że (komentarze w nawiasach moje):
Jeżeli w zdaniu zastąpimy pojęcie jego (poprawną) redefinicją, to zdanie to zachowa (musi) swoje znaczenie.
Co to znaczy? Popatrzmy. Słownikowa definicja psa (SJP):
pies: zwierzę domowe hodowane m.in. dla przyjemności lub do polowań
A teraz relacja z wydarzenia (zdanie):
Pies szczeka na listonosza.
Testujemy definicję psa:
Jeżeli jest prawdą, że:
pies to zwierzę domowe hodowane m.in. dla przyjemności lub do polowań
to jest także prawdą (to zdanie zachowuje swoje znaczenie):
Zwierzę domowe hodowane m.in. dla przyjemności lub do polowań, szczeka na listonosza.
Inny przykład.
samochód: pojazd na kołach napędzany silnikiem, służący do przewozu osób lub ładunków
Relacja świadka:
Samochód potrącił pieszego na skrzyżowaniu
A więc można także powiedzieć, że:
Pojazd na kołach napędzany silnikiem, służący do przewozu osób lub ładunków, potrącił pieszego na skrzyżowaniu
Obszerny opis znajdzie czytelnik w artykule Ontologia czyli jak się to robi.
Bibliografia
Haelle, T. (2013, March 12). What Is the Answer to That Stupid Math Problem on Facebook? Slate. https://slate.com/technology/2013/03/facebook-math-problem-why-pemdas-doesnt-always-give-a-clear-answer.html
Hołówka, T. (2012). Kultura logiczna w przykładach (Wydawnictwo Naukowe PWN, Ed.). Wydawnictwo Naukowe PWN.
Boisseau, G., Bonchi, F., Di Giorgio, A., & Sobocinski, P. (2021). Diagrammatic Polyhedral Algebra. arXiv:2105.10946 [Cs, Math]. http://arxiv.org/abs/2105.10946
Dörfler, W. (2005). Diagrammatic Thinking. In M. H. G. Hoffmann, J. Lenhard, & F. Seeger (Eds.), Activity and Sign (pp. 57–66). Springer-Verlag. https://doi.org/10.1007/0-387-24270-8_6
Lloyd, K. (2018). Foundational Concepts Underlying a Formal Mathematical Basis for Systems Science. Proceedings of the 62nd Annual Meeting of the ISSS – 2018 Corvallis, OR, USA, 1(1). http://journals.isss.org/index.php/proceedings62nd/article/view/3363
Subbotin A.L. (1970). Idealization as a Method of Scientific Knowledge. In Tavanec P.V. (eds) Problems of the Logic of Scientific Knowledge. Synthese Library.
Primiero, G. (2016). Information in the philosophy of computer science. The Routledge Handbook of Philosophy of Information, 90–106.
Cleland, C. E. (2011). Nauki historyczne, nauki eksperymentalne i metoda naukowa. Filozoficzne Aspekty Genezy, 8, 105–120. http://cejsh.icm.edu.pl/cejsh/element/bwmeta1.element.desklight-e1d62e83-4750-49a5-b603-ee7c98e5d806
Ufnalska, S. T. (2013). Wskazówki EASE (Europejskiego Stowarzyszenia Redaktorów Naukowych) dla autorów i tłumaczy artykułów naukowych publikowanych w jezyku angielskim. https://delibra.bg.polsl.pl/dlibra/doccontent?id=15440





