Wprowadzenie
Niedawno pisałem o pewnej innej książce, jej autor opisał systemowe podejście do analizy przedsiębiorstwa. Napisałem między innymi wtedy, że:
Rzecz w tym, że pojęcie ?analiza systemowa? jest używane najczęściej (jak obserwuję, prawie zawsze) w znaczeniu analizy i projektowania oprogramowania (systemy IT) co jest błędem.Tak zwane ?całościowe myślenie? (holistyczne) to uznanie, że system to nie tylko oprogramowanie. (Źródło: Systems Thinking czyli analiza systemowa organizacji | Jarosław Żeliński IT-Consulting)
Tak więc pora na ciąg dalszy.
Ogólna Teoria Systemów
Książka ta, Ogólna Teoria Systemów , czekała u mnie na swój czas, i doczekała się. Literatura o teorii systemów nie jest zbyt bogata niestety, w Polsce to głównie pozycje Sienkiewicza, Cempela , i chyba najbogatsza w treść praca zbiorowa pod kierunkiem Findeisena . Dla tych, którzy nie wiedzą, ogólna teoria systemów to dzieło biologa (Ludwig von Bertalanffy). Egzemplarz książki, który mam przed sobą, to dwudzieste papierowe wydanie! Teraz więc pora na książkę twórcy tej teorii.
Nie będę tym razem streszczał ani oceniał tej książki, po prostu każdy kto ma słowo “System” w nazwie zawodu lub zakresie obowiązków, i chce tę “pracę” wykonywać z pełnym zrozumieniem i dobrze, powinien tę teorie znać i rozumieć. Tu tylko pokażę “o co chodzi”.
Definicja systemu w różnych, ale bardzo bliskich sobie, formach brzmi:
złożony obiekt wyróżniony w badanej rzeczywistości, stanowiący całość tworzoną przez zbiór obiektów elementarnych (elementów) i powiązań (związków i relacji) między nimi
System bywa także nazywany “zorganizowaną złożonością”. Klasyczna ogólna teoria systemów oparta jest na matematycznych modelach (równaniach), opisujących reakcję każdego elementu systemu, i systemu jako całość, na określone bodźce. Mechanizm działania (zachowania się) systemu to wynikowy “wzór”. W metodzie naukowej zestaw takich matematycznych równań nazywa się “modelem” lub po prostu teorią wyjaśniającą. Równania opisujące te elementy to, zależnie od złożoności systemu, [[równania liniowe]] (proste) lub [[równania nieliniowe]]. W kolejnych akapitach wyjaśnię jaki to ma związek (a ma!) z modelowaniem organizacji.
Klasyfikacja matematyczna systemów jak problemów do rozwiązania (źródło: recenzowana książka):
Powyższa tablica pokazuje zestawienie rodzajów równań wymaganych do opisania zachowania systemu. Wiersze to kolejno proste równania algebraiczne, proste i złożone równania różniczkowe. W kolumnach mamy ilość równań (układ równań) opisujących dany system (odpowiada to złożoności całego badanego systemu).
“Banalnie proste” systemy można opisać jednym, prostym równaniem liniowym. Systemy uznawane za “łatwe” do analizy to te, dające się opisać prostym układem kilku równań liniowych lub jednym równaniem różniczkowym. Systemy wymagające do ich opisu (zamodelowania) układu bardzo wielu równań liniowych lub nawet kilku pojedynczych różniczkowych, stają bardzo trudne, a w miarę rosnącej ilości równań (złożoności systemu), są po prostu niemożliwe do rozwiązania metodą inną niż statystyczna (iteracje i badanie rezultatów). Pisząc “analiza” mamy tu na myśli możliwość nie tylko opisania tymi równaniami systemu (bo to nie musi być trudne) ale ich (tych równań) rozwiązanie (przypominam: to wiele równań z wieloma zmiennymi).
Uczenie maszynowe i “sztuczna inteligencja”
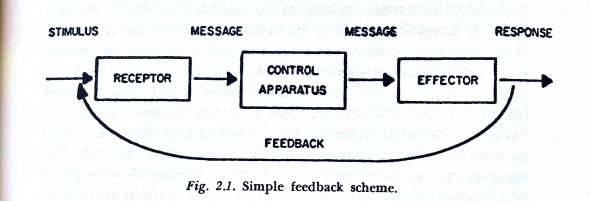
Idźmy dalej :). Podstawowym modelem systemu otwartego jest układ sprzężenia zwrotnego (źr. opisywana książka):
Diagram może wygląda dość anachronicznie ale pamiętajmy, że książkę napisano w 1969 roku. Nie zmienia to faktu, że tak właśnie wygląda ogólny model systemu. Jest to system otwarty, to znaczy taki, który ma interakcje ze swoim otoczeniem (system zamknięty nie ma takich interakcji, takich nie będziemy tu rozpatrywali).
System adaptacyjny
A teraz popatrzmy na prosty, elementarny, model systemu otwartego wykonanego z użyciem notacji UML :
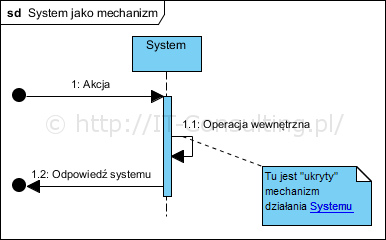
Każdy system można zdefiniować jako “jakiś mechanizm”, który “jakoś” reaguje na bodźce. Gdy mówimy o tak zwanej metodzie naukowej analizy to znaczy, że stawiamy hipotezę wyjaśniającą zachowanie systemu. Ta hipoteza to nic innego jak model tego systemu czyli opis mechanizmu jego działania. Teoria naukowa (tak zwana teoria wyjaśniająca) to model pozwalający na wyjaśnienie zaobserwowanych (nie musi ich być wiele) zachowań systemu i przewidywanie przyszłych jego zachowań (reakcji na bodźce). Teoria taka jest uznawana za poprawną do czasu wskazania zachowania (reakcji na bodziec), którego model (teoria) nie wyjaśnia (to nazywamy falsyfikacją teorii) .
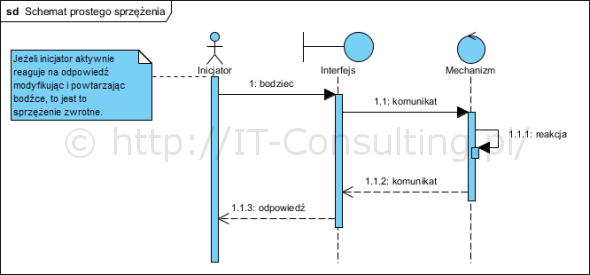
Pokażmy powyższy model w “nowej postaci”, w notacji UML, sprzężenie zwrotne uwidocznione na diagramie z książki, może wyglądać tak:
Powyższy diagram UML jest odwzorowaniem prezentowanego (cytowanego) powyżej diagramu obrazującego sprzężenie zwrotne. Mam nadzieję, że widać podobieństwo do, nie raz tu (w moim blogu) prezentowanych, modeli opisujących scenariusz przypadku użycia (który jest bodźcem inicjowanym przez aktora). Powyższy diagram, to prosty system, który ma pewną cechę: każdy kolejny taki sam bodziec spowoduje dokładnie taką samą reakcję systemu. Niestety taki model nie nadaje się do większości zastosowań związanych z tak zwanym biznesem, i nie tylko. Dlaczego? Ten model to wyjaśni:
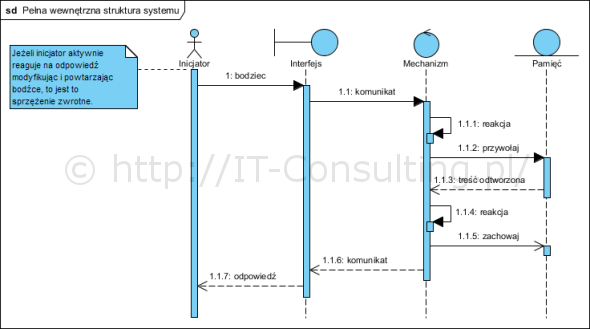
Tu mamy tak zwany model systemu z pamięcią. Eureka :), to nasze aplikacje. Systemy społeczne spotykane wokół nas to z reguły systemy z pamięcią, kolejne reakcje systemu to efekt bodźca jaki się pojawi i wcześniejszych zapamiętanych reakcji (historii). Jak widać takie same bodźce mogą wywoływać inne reakcje w przypadku systemu z pamięcią. Tak działamy my (uczymy się), tak działa większość aplikacji biznesowych (zbiera dane). Systemów bez pamięci także mamy wokół sobie wiele. Od zegarka czy prostego kalkulatora (wyniki podstawowych operacji matematycznych nie zależą historii obliczeń) do robotów kuchennych i wielu podobnych, nawet nie raz bardzo złożonych elementów gospodarstwa domowego i nie tylko.
Jeżeli reakcja będzie (1.1.4.) będzie nie tylko prostym zachowaniem wyniku, ale także algorytmem modyfikującym zawartość pamięci, to powyższy schemat opisuje tak zwane systemy “uczące się” (machine learning), które obecnie nazywane są sztuczna inteligencją. Poniższy diagram pokazuje powyższe w postaci znanej z podręczników:
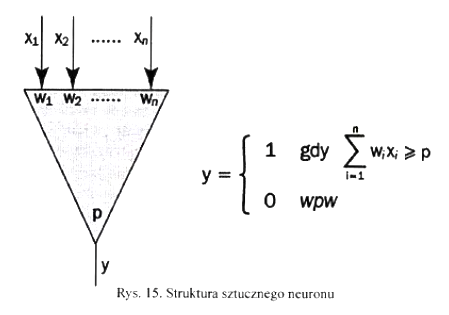
Na powyższym przykładzie widać także między zapisem matematycznym a opisanym modelem: tu stwierdzono, że jest to “jakaś” funkcja y=f(X1, X2,…Xn), wyżej opisany model pokazuje mechanizm powstawania wyniku (ta funkcja tego nie pokazuje).
Nieco inną próbę tworzenia modelu cybernetycznego z użyciem UML pojęli Panetto i Petin .
Popatrzmy na ogólny schemat uczenia sieci neuronowej:
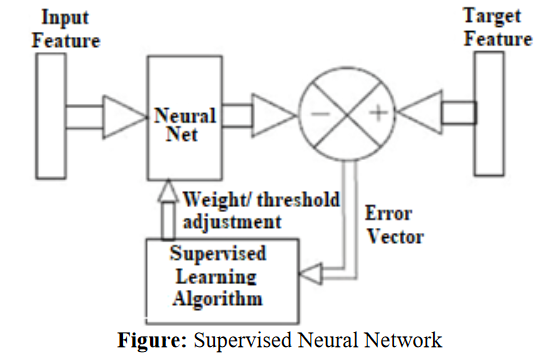
Jak widać jest to typowy system ze sprzężeniem zwrotnym. To co popularnie nazywamy sztuczną inteligencją, to tylko rozbudowane modele statystyczne oraz algorytmy, które z nich korzystają do generowania odpowiedzi (Target Feature).
Uczenie takich modeli wymaga ogromnych mocy obliczeniowych i ogromnych ilości danych oraz nie miej ogromnych ilości operacji porównania z wzorcem, które idą w miliony, a nie raz miliardy. Powyższe można uogólnić do postaci:
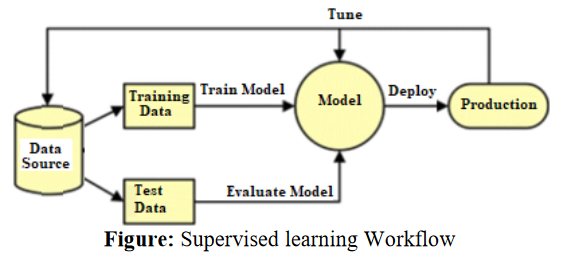
Korzystanie z AI to korzystanie z tak wytworzonego Modelu (a w zasadzie modelu i danych powstałych w procesie uczenia). Polega to na “zadaniu pytania” (prompt) i oczekiwaniu na wyniki. Wynik działania modelu może być dodatkowo przetwarzany (Production) np. w celu skomponowania “ludzko brzmiącej” odpowiedzi na prompt (polecenie, zapytanie) czyli tekstu, obrazu czy dźwięku. Tu w użyciu są algorytmy znane z oprogramowania do edycji tych mediów. Dokładnie w ten sposób, od wielu lat, działają np. systemy do generowania maszynowych tłumaczeń czy kontroli ortografii.
Biznes jako system
Jakim rodzajem systemu jest aplikacja biznesowa? Mamy tu – w biznesie – w zasadzie wyłącznie proste operacje matematyczne (równania liniowe) takie jak wyliczanie wartości, podatku VAT i sumy do zapłaty fakturach, wielkości obrotów w miesiącu czy roku, sald kont itp. Złożoność aplikacji biznesowych tkwi w ilości prostych obliczeń i liczby ich wzajemnych zależności (układy wielu równań liniowych). Model obiektowy (jak najbardziej adekwatny do modelowania systemów, biznesowych też) to takie “atomowe” obiekty “systemy”, każdy z operacjami (metoda: mechanizm reagowania obiektu na bodziec czyli na komunikat do niego kierowany) i pamięcią (wartości atrybutów). Projektowanie (porządkowanie) architektury aplikacji to panowanie nad złożonością całego takiego systemu, pilnowanie by jego opis nie stał się układem wielu równań nieliniowych (unikanie wewnętrznych sprzężeń, wywołań “wiele do wielu” itp. czyli tak zwanego “spaghetti”).
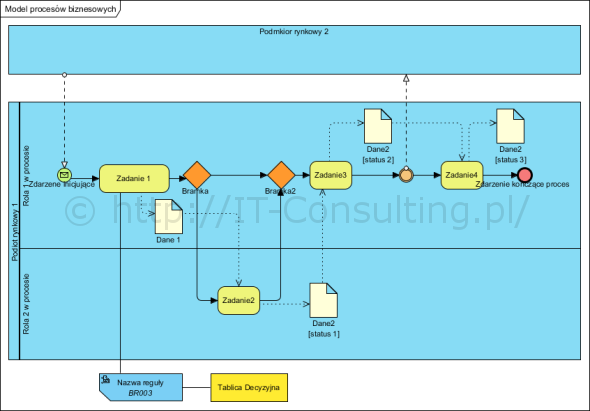
Przy próbach modelowania złożonych systemów składających się z ludzi i ich narzędzi pracy zaczynają się problemy. Organizacje modelujemy na pewnym poziomie ogólności, takim by abstrahować od specyfiki konkretnych przypadków i warunków i realizacji, te szczegóły (zmienne) jesteśmy zmuszeni pominąć, gdyż w przeciwnym wypadku poprawny model nie byłby w stanie powstać z uwagi na jego złożoność. Tu model pokazuje kluczowe zachowania, o których wiemy, że muszą się pojawić i są przewidywalne (bo. np. wymuszone prawem, regulaminem itp.). Model organizacji, dający się testować musi więc pomijać wszelkie szczegóły, specyficzne dla konkretnej sytuacji. Poziom złożoności modelu procesu biznesowego powinien więc utrzymywać taką postać (notacja BPMN) :
Z uwagi na przyjmowaną powszechnie definicję procesu: aktywność tworząca wartość, przekształcając stan wejścia w stan wyjścia, na modelu takim muszą być uwidocznione produkty każdej aktywności (i jej wejścia). Więcej o modelowaniu procesów biznesowych można przeczytać w innych publikowanych tu artykułach.
W toku analizy i projektowania kluczowym elementem jest testowanie modeli. Model to hipoteza brzmiąca: “tak to działa”. Zarówno model scenariusza przypadku użycia (diagram sekwencji, bo tylko te się testuje, diagramy przypadków użycia to lista usług a nie ich realizacje, tu możemy testować najwyżej ich kompletność), jak i wcześniej opracowane modele procesów biznesowych, się testuje. Test taki polega na próbie wykazania wad (próba falsyfikacji) modelu. Odbiór takiej dokumentacji nie polega więc (nie powinien) na udowadnianiu przez autora (jak?), że to dobry model, polega na próbie wskazania wad dokumentacji (np. odbiorca wskaże w organizacji działania, których nie opisuje model). Dokładnie tak samo przebiegają testy akceptacyjne dostarczonego oprogramowania: oprogramowanie jest dobre, chyba że w toku testów (skończonej ich ilości!) nie zadziała ono zgodnie z opisanym wymaganiem (zadeklarowanym rezultatem).
Systemy społeczne, z uwagi na ogrom czynników mających wpływ na nie, można opisywać wyłącznie statystycznie a ich modele są jedynie przybliżone, nie są to teorie w ścisłym tego słowa znaczeniu (np. tak zwane prawo popytu i podaży nie jest teorią naukową) bo nie da się przewidywać zachowania takiego systemu, nie da się nawet wyliczyć prawdopodobieństwa tego co i czy się wydarzy, można co najwyżej oszacować (w zasadzie jest to bardziej wróżba) i czekać. Opisałem to przy okazji komentowania mody na big data.
Niestety otwarte systemy złożone takie jak społeczeństwa, rynki czy nawet złożone aplikacje to złożoność opisana w prawej dolnej części tabeli na początku tego tekstu. Są to systemy dla nas nieprzewidywalne, można mówić o zrozumieniu konkretnych ich elementów ale nie o “rozwiązywaniu całości”. To jak chmury, znamy zasady termodynamiki, budowę atomów i cząstek pary wodnej, ale złożoność np. chmury burzowej (liczba nieliniowych równań ja opisujących) to taki “układ równań” niemożliwy do rozwiązania, można mówić co najwyżej o iteracyjnym “podstawianiu”, i tak działają symulatory pogody (te prognozy nadal, jak wiemy, są krótko terminowe i obarczone nie małym błędem). Analogiczna sytuacja ma miejsce np. na giełdach walut czy akcji, prognozowanie ich kursów to loteria (co wykazano w nauce nie raz, a mimo to entuzjaści analizy technicznej nie wierzą ;)).
Tak więc organizacja, która planuje zakup i wdrożenie oprogramowania, to system składający się z ludzi, mechanizmów ich działania (ich umiejętności i zakresy obowiązków, stawiane zadania) oraz narzędzi pracy, które także są systemami: to oprogramowanie i ich środowisko. Czy można przewidywać ich zachowanie? Nie. Ale można opracować model takiej organizacji i ze zrozumieniem starać się nią kierować ([[podejmowanie decyzji]]). Wymagania na oprogramowanie może być listą oczekiwań przyszłych użytkowników ale to stanowczo za mało, skuteczne wymaganie to żądany model systemu jakim jest planowana do wdrożenia aplikacja.
Szukając gotowego oprogramowania na rynku, tworzymy ogólniejszy model tego co potrzebujemy (bloki funkcjonalne, komponenty) i szukamy, i raczej będą to dobrane dziedzinowe aplikacje niż jeden monolit pasujący do modelu naszej organizacji … Teraz, mam nadzieję, wiemy dlaczego nietrywialne oprogramowanie, dla osiągnięcia wysokiej jego jakości, musimy testować (iteracyjne podawanie bodźców) bo nie jest możliwe udowodnienie (wyliczenie) tego na podstawie tylko treści kodu.
A teraz zachęcam do lektury książki, otworzy oczy na wiele zjawisk które wokół siebie obserwujemy.